알고리즘 분할정복2

합병정렬

“데이터 집합 두 개를 하나로 합치는 과정”을 하나의 데이터 집합이 남을 때까지 반복 단, 합병 대상의 데이터 집합이 미리 정복되어 있어야 한다!

merge_sort

void merge_sort_DC(int list[], int low, int high)
{
  int middle;
  if(low<high)
  {
    middle = (low + high)/2;
    merge_sort_DC(list,low,middle);
    merge_sort_DC(list,middle+1, high);
    merge(list,low,middle,high);
  }
}

void merge(int list[], int low, int mid, int high)
{
  int n1 = low, n2 = mid+1, s=low, sorted[MAX_SIZE], i;
  while(n1 <= mid && n2 <= high)
  {
    if(list[n1] <= list[n2]) sorted[s++] = list[n1++];
    else sorted[s++] = list[n2++];
  }

  if(n1 > mid)while(n2 <= high) sorted[s++] = list[n2++];
  else while(n1<=mid)sorted[s++] = list[n1++];
  for(i = low; i <= high;i++) list[i] = sorted[i];
}

마스터 정리

T(n) = 2T(n/2) + Θ(n) a=b^c인 경우, 따라서 T(n) = Θ(nlogn)
비교 연산 횟수

트리의 모든 레벨에서 비교 연산은 동일하게 Θ(n)이고 트리의 높이는 Θ(logn)이므로 합병정렬의 점근 복잡도는 Θ(nlogn)
제자리 정렬 알고리즘
- 입력 데이터의 개수와 무관한 메모리 공간을 추가적으로 사용
- 합병정렬은 Θ(n)의 공간을 필요로 하기 때문에 제자리 정렬이 아니다.

퀵정렬

전체 데이터 집합을 두 개의 집합으로 분할하고 각각의 데이터 집합을 퀵정렬, 부문제가 두 개인데 결합 과정이 없음

quick_sort

source:wikipedia

분할 과정에서 배열의 모든 원소는 한번씩 스캔해야 하므로 Θ(n)

최선의 경우

T(n) = 2T(n/2) + Θ(n) 순환 호출 트리의 높이가 최대한 낮아야 함 합병 정렬처럼 분할이 절반씩 이루어져야함 마스터 정리에 따라 T(n) = Θ(nlogn)
최악의 경우

분할이 완전히 불균형 적으로 일어나서 매번 한쪽은 원소가 아예 없는 경우 예를 들어 처음 부터 정렬되어있거나 역으로 정렬되있는 경우가 있다. 트리의 높이가 Θ(n) 시간 복잡도는 Θ(n^2)

평균적인 경우

(피벗의 왼쪽 원소의 개수, 피벗의 오른쪽 원소의 개수) = (i, n-i-1)따라서 T(n) = T(i) + T(n-i-1) + Θ(n) 복잡도는T(n) = Θ(nlogn)
분석 결과

최악의 경우는 정렬된 상태 단 한가지 밖에 없기 때문에 복잡도는 보통 Θ(nlogn)이라고 한다.
퀵정렬의 더욱 빠르게(더 좋은 피봇을 선택한다면?)
- median of medians
  
  정확히 절반을 가르는 O(n)의 선택 알고리즘을 사용한다면 퀵정렬은 Θ(nlogn) 그러나 실제 측정해보면 단순하게 선택하는 알고리즘 보다 느리다.
- median of three
  
  배열의 세 원소중 중간값을 피봇으로 선택하는 방법, O(1)의 단순한 전략이지만 절대로 최악의 경우를 만들어 내지 않는다.
퀵 정렬은 제자리 정렬인가?

System stack을 따진다면 제자리 정렬이 아니지만 따지지 않는다면 제자리 정렬이다.
임계값의 선택

Threshold를 낮춘다면 단순한 형태의 알고리즘이 탄생하지만 효율성이 낮고, 반대로 높인다면 효율성이 증가하고 불필요한 함수 호출을 피할 수 있다. 효율성을 극대화 하기위해 퀵정렬과 삽입정렬을 함께 사용하는 하이브리드 알고리즘을 쓰기도 한다.

트로미노 타일로 체스판 채우기

구멍이 하나 있는 정사각형 체스판을 L자 모양의 트로미노 타일로 채울 수 있는가? 체스판의 크기를 2^k x 2^k라 가정, 수학적 귀납법을 설명하는데 자주 사용되는 예제다.

가장 작은 크기의 부문제인 “구멍이 하나 있는 2 x 2 체스판”에 대해 어느곳에 구멍이 있더라도 체스판을 채우는 것이 가능한가를 확인 한다.
“구멍이 하나 있는 2^k x 2^k 체스판”에서 “구멍이 하나 있는 2 x 2 체스판”으로 문제를 점차 줄여나갈 수만 있다면 분할 정복 알고리즘을 사용하여 해결 가능하다.

복잡도 분석
- 체스판의 차원 n기준으로
부문제는 매번 4개이고, 문제의 크기는 절반으로 줄어든다. 순환 호출 전 4개의 배열로 나누고 순환 호출 후 배열 board로 모으는 작업이 필요하므로 분할과 결합에 체스판 원소 개수에 비례하는 Θ(n^2)이 걸린다. (2차원 배열을 하나 더쓰기 때문) T(n) = 4T(n/2) + Θ(n^2)마스터 정리에 따르면 Θ(n^2logn)
- 체스판의 지수 K를 기준으로
부문제는 4개이고 k는 1씩 줄어든다 분할과 결합에 체스판 원소 개수 2^k x 2^k에 비례하는 Θ(2^(2k))가 걸린다. T(k) = 4T(k-1) + Θ(2^(2k))는 마스터 정리를 사용할 수 없으므로 점화식을 대입법을 사용하여 푼다.

하노이탑

하노이의 탑(Tower of Hanoi)은 퍼즐의 일종이다. 세 개의 기둥과 이 기둥에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있다.

게임의 목적은 다음 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것이다.

한 번에 하나의 원판만 옮길 수 있다.
큰 원판이 작은 원판 위에 있어서는 안 된다.

알고리즘

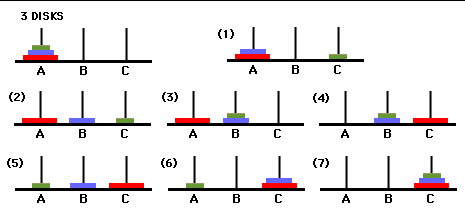hanoi source:codewithc.com

3 막대를 각각 from(A), temp(B), to(C)라 하고 원판은 최초에 from에 있으며 최종적으로 to로 옮기는 것으로 가정

from(A)의 n-1개의 원판을 to(C)를 이용하여 temp(B)로 옮기기
from(A)의 원판을 to(C)로 옮기기
temp(B)의 n-1개의 원판을 from(A)을 이용하여 to로 옮기기

복잡도 분석

실행 시간 기준

부 문제는 2개이고 문제 크기는 1씩 줄어들고 분할과 결합에는 특별한 시간이 걸리지 않으므로 T(n) = 2T(n-1) + O(1)
이동 횟수 기준

C(n):n개의 원판을 옮기는데 걸리는 총 이동 횟수
```
  C(n) = C(n-1) + 1 + C(n-1)
           = 2C(n-1) + 1
           = 2(2C(n-2) + 1) + 1
           = 2(2(2C(n-3)) + 1) + 1) + 1
           .
           .
           .
           = 2^n - 1
           =Θ(2^n)
```
함수를 실행할 때마다 두 번의 순환 호출을 하게 되는데 문제의 크기가 1 만큼만 줄어들기 때문에 시간 복잡도는 상당히 높을 수밖에 없다.

분할 정복을 마치며

분할 정복 알고리즘
- 부문제의 정복은 순환 호출에 의존
- 부문제는 해결되었다고 보고 부문제를 어떻게 풀지 고민하지 않음
- 효율성 문제를 보완하려면 스택의 순환 구조를 스택의 반복 구조로 변환
분할 정복 기법을 사용하면 좋지 않은 경우?
- 부문제가 커지는 경우
- 두 개 이상의 부문제로 나누어지지만, 부문제의 크기가 거의 변하지 않는 경우
  
  피보나치 수열 계산 알고리즘 : 두 개의 부문제로 나누어지지만, 각 부문제의 크기는 n-1과 n-2…
- 동일한 부문제들이 자주 등장하는 경우
  
  분할정복은 모두 부문제들을 독립적으로 해결해야 하고 부문제들이 중첩되는 경우는 비효율적이다. 피보나치 수열 문제는 부문제의 크기도 조금씩 줄어들고 동일한 부문제들도 자주 등장