컴퓨터 구조 floating point

Floating Point

real numbers( float in C)

1.0 * 2^-1 = 10.0 * 2^-2 = 0.1 * 2^0

binary point is not fixed (floating)

normalized number : 1.xxx * 2^yyy

---

Float point representation

(-1)^S * (1 + fraction) * 2^(exponent - bias)

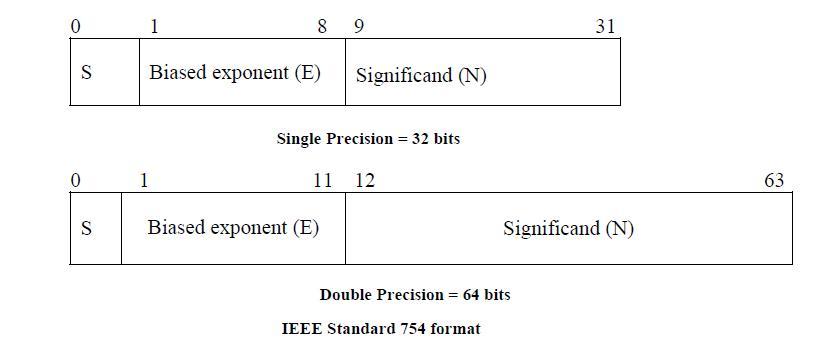
• single precision

  bias = 127

  -0.75----dec = -11 * 2^(-2)----binary
  
  -1.1 * 2^(-1)
  
  S : 1, fraction : 10000...0(23bits), exponent : -1 + 127 = 0111 1110
  
  1 | 0111 1110 | 1000...00 (23bits)|
  

• double precision

  bias = 1024

  -0.75
  
  S : 1, fraction : 1000...000 (52bits), exponent : 011 1111 1110
  

1|1000 0001|0100...0| ---- single precision

-1.01 * 2^2

---

Floating point Addition

0.5 + (-0.4375)?---(decimal)

0.5 = 1.000 * 2^-1

-0.4375(10) = -7/16 (2)= -111 * 2^-4 = -1.110 * 2^-2

1. compare the exponents and shifts the smaller number to the right -1.110 * 2^-2 = -0.11 * 2^-1

2. Add (1.000 + (-0.111)) * 2 ^ -1 = 0.001 * 2 ^ -1 = 1.000 * 2^-4

3. Check for overflow or underflow -4는 -126~127사이이기 때문에 exponent 표현이 가능합니다. no oveflow, underflow

4. Check 4 bit precision 1.000 * 2 ^ -4

---

exponent of the product : adding the components

(1.000 * 2 ^ -1) * (-1.110 * 2 ^ -2)

1. add exponents -1 + (-2) = -3

2. product 1.000 * 1.110 = 1.110000

3. Check for overflow or underflow -3은 -126 ~ 127사이 입니다.

4. Check sign, 4bit precision 1.110 * 2 ^ -3

---

exercise

• -1.25 single, double

  -1.25 = -5/4 = -101/2^2 = -1.01 * 2^0
  
  single
  -------
  S : 1
  exponent : 0111 1111
  fraction : 01000...000(23bits)
  
  double
  -------
  S : 1
  exponent : 130 - 127 = 3
  fraction : 010100...0(52bits)
  

• 110000010010100…0 -> what number?(single) -1.0101 * 2^3

  sign : 1
  exponent : 130-127 = 3
  fraction : 010100...0(23bits)
  

• 0.375 + 1.5 = ?

  0.75 = 3 / 2^3 = 1.1 * 2^-2
  1.5 = 3 / 2 = 1.1 * 2^0
  
  1. 1.1 * 2^-2 -> 0.011 * 2^0
  2. 1.1 * 2^0 + 0.011 * 2^0 = 1.111 * 2^0
  3. -126 <= 0(exponent) <= 127
  4. 1.111 * 2^0
  

• 1.010(2) * 0101(2) = ?

  (1.010 * 2^0) * (1.01 * 2^2)
  1. add exponent (2 + 0)
  2. 1.010 * 1.01 = 1.100100
  3. -126<=2(exponent)<=127
  4. check sign and 4 bits precision 1.100 * 2^2